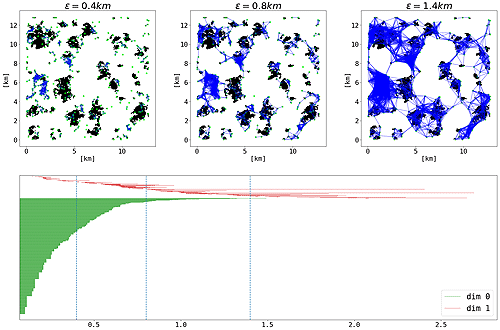
| Illustration 1: An example of a Vietoris-Rips filtration, a geometric object central to TDA, constructed using point data from a shallow cumulus cloud field (top row). Also shown is its corresponding barcode, one representation of the information extracted by using persistent homology (bottom). Image author: Jose L. Licon Salaiz |
Event name: Summer School on Topological Data Analysis and Persistent Homology
Event dates: June 11th – 15th, 2018
Event location: Levico Terme, Italy
Author name: José Luis Licón Saláiz, PhD student at University of Cologne, Mathematical Inst.
Author project: C7
This summer school was a one-week gathering of researchers and students in the area of topological data anlysis (TDA) to discuss the current state of the field. Every day consisted of two theoretical lectures and one practical session, where the theory was illustrated using software and real-world data. The lecturers were John Harer (Duke University) and Steve Oudot (INRIA Saclay), and they covered subjects ranging from algorithms for TDA, its connections to statistics and machine learning, and a category-theoretical view on persistent homology aimed at generalizing to multidimensional persistence. Attending the school was particularly beneficial because, as the field is very new and rapidly evolving, it is hard to get a good overview of all the theory and techniques involved. This is important for me because I am currently using TDA to study the spatial structure of atmospheric turbulence and the distribution of cloud fields. It was also a good opportunity to exchange ideas with other young researchers, especially Henri Riihimäki (Tampere Unviersity of Technology/KTH Stockholm), with whom I am working on the statistical representation of topological information, and Grzegorz Muszynski (Lawrence Livermore National Laboratory), who is using TDA to detect patterns in large-scale climate models.